Parabolan War (Guide)/Warplan

This calculator will guide you through a Campaign of Parabolan Warfare by deciding the correct options to play at each Stage and values of and , based on your character's stats and your own valuation of the different items that might be consumed.

By using this calculator, you are making the decision that you would rather let a spreadsheet play the game for you. You should only use this tool if you already find grinds to be joyless, or a higher EPA is better motivation than gameplay.

This calculator is considered Beta-quality. As far as I can tell it probably works right, but if something seems odd, then send questions or bugs to my Talk page. It also makes the hamster-wheel in the server spin really fast. Know Beta things:

• The tables are not collapsible in this page. They will be collapsible if you output as Wikitext and save to your user page.
• Options that use Advanced Skills are not implemented.

Using this Calculator

The first set of inputs is straightforward: your character's stats, and your choice of Campaign and General. The choice of campaign only affects the number of actions spent on narrative after each stage.

The second set of inputs is the Action costs for the various items that can be spent (or gained) via the various actions on the campaign trial. This calculator works by converting all resources into an "action cost" equivalent, so items are valued based on the number of actions to replenish those spent. are valued based on the actions to clear them after the campaign. The default values assume all resources can be obtained at 2.5 EPA, and that Ravages take 1 action to clear.

The results of the calculator will show tables of the expected actions to complete the Parabolan Campaign from any given campaign state, as well as the optimal choice at each state. If Airs-dependent actions are worth playing, then the tables will list the best non-Airs choice, as well as all Airs-dependent choices that should be played if available.

In some cases, multiple choices are equally-optimal. Ties are broken by arbitrary implementation details.

By default, the calculator will display your Battle-Plan on this page. Save your Battle-Plan to your own user pages by selecting the output format of "WikiCode" and copy-pasting the resulting Wiki mark-up into your own page.

Get My Personalized Battle-Plan

 template = :Parabolan War (Guide)/Saver
 form = parameters
 result = warplan
  param = Campaign|Campaign|Yourself|select|Viscountess,Ophidian Gentleman,Second City Priest,The Cats,The Fingerkings,The Chessboard,Yourself|The Cats,The Fingerkings,The Chessboard=General,General_Level
 param = General|Chosen General|None|buttonselect|None,Cat,Snake,Chess
 param = General_Level|General Level|3|buttonselect|1,2,3
 param = selects|Character Stats||group|Watchful,Shadowy,Dangerous,Persuasive,Glasswork,Toxicology,Mithridacy,Chess,Silverer
 param = Watchful|Watchful|300|int|0-400
 param = Shadowy|Shadowy|300|int|0-400
 param = Dangerous|Dangerous|300|int|0-400
 param = Persuasive|Persuasive|300|int|0-400
 param = Glasswork|Glasswork|7|int|0-20
 param = Toxicology|Kataleptic Toxicology|7|int|0-20
 param = Mithridacy|Mithridacy|7|int|0-20
 param = Chess|A Player of Chess|7|int|0-20
 param = Silverer|Silverer?|no|check|yes,no
 param = selects|Item Costs, in Actions to Acquire||group|Cost_Ravage,Cost_Psalm,Cost_Sign,Cost_Self,Cost_Glass,Cost_Wing,Cost_Plaque,Cost_Light,Cost_Solacefruit,Cost_Viric,Cost_Feather,Cost_Claw,Cost_Address,Cost_Palim,Cost_Pawn,Cost_Move,Cost_Nightmare,Cost_Catch
 param = Cost_Ravage|Curing Ravages of Parabolan Warfare|1|number|0-10
 param = Cost_Nightmare|Curing 1 CP of Nightmares|0.5|number|0-10
 param = Cost_Psalm|Apostate's Psalm|1|number|0-10
 param = Cost_Sign|London Street Sign|1|number|0-10
 param = Cost_Self|Memory of a Much Lesser Self|1|number|0-10
 param = Cost_Glass|Glass Gazette|1|number|0-10
 param = Cost_Wing|Wing of a Young Terror Bird|1|number|0-10
 param = Cost_Plaque|Correspondence Plaque|0.2|number|0-10
 param = Cost_Catch|Deep-Zee Catch|0.2|number|0-10
 param = Cost_Light|Memory of Light|0.2|number|0-10
 param = Cost_Move|Moves in the Great Game|0.2|number|0-10
 param = Cost_Palim|Palimpsest Scrap|0.2|number|0-10
 param = Cost_Address|Secluded Address|0.2|number|0-10
 param = Cost_Solacefruit|Solacefruit|0.2|number|0-10
 param = Cost_Viric|Trace of Viric|0.2|number|0-10
 param = Cost_Feather|Royal-Blue Feather|0.2|number|0-10
 param = Cost_Claw|Silvered Cat's Claw|0.04|number|0-10
 param = Cost_Pawn|Well-Placed Pawns|0.04|number|0-10
 param = Format|Output Format|Tables|buttonselect|Tables,WikiCode

Fingerkings loading...

 

How it Works

This calculator is based on a classical optimization technique called Dynamic Programming. (Despite the similar name, this bears no relation to "dynamic programming languages" like JavaScript or Lua.) The core concept is that results are computed starting from the end of the campaign working backwards rather than from the beginning, calculating actions-to-goal rather than actions-spent. Going in this order means that when considering any given campaign state, the outcomes of the all of the options available from that state have already been calculated, so the arithmetic to choose which is best becomes very simple.

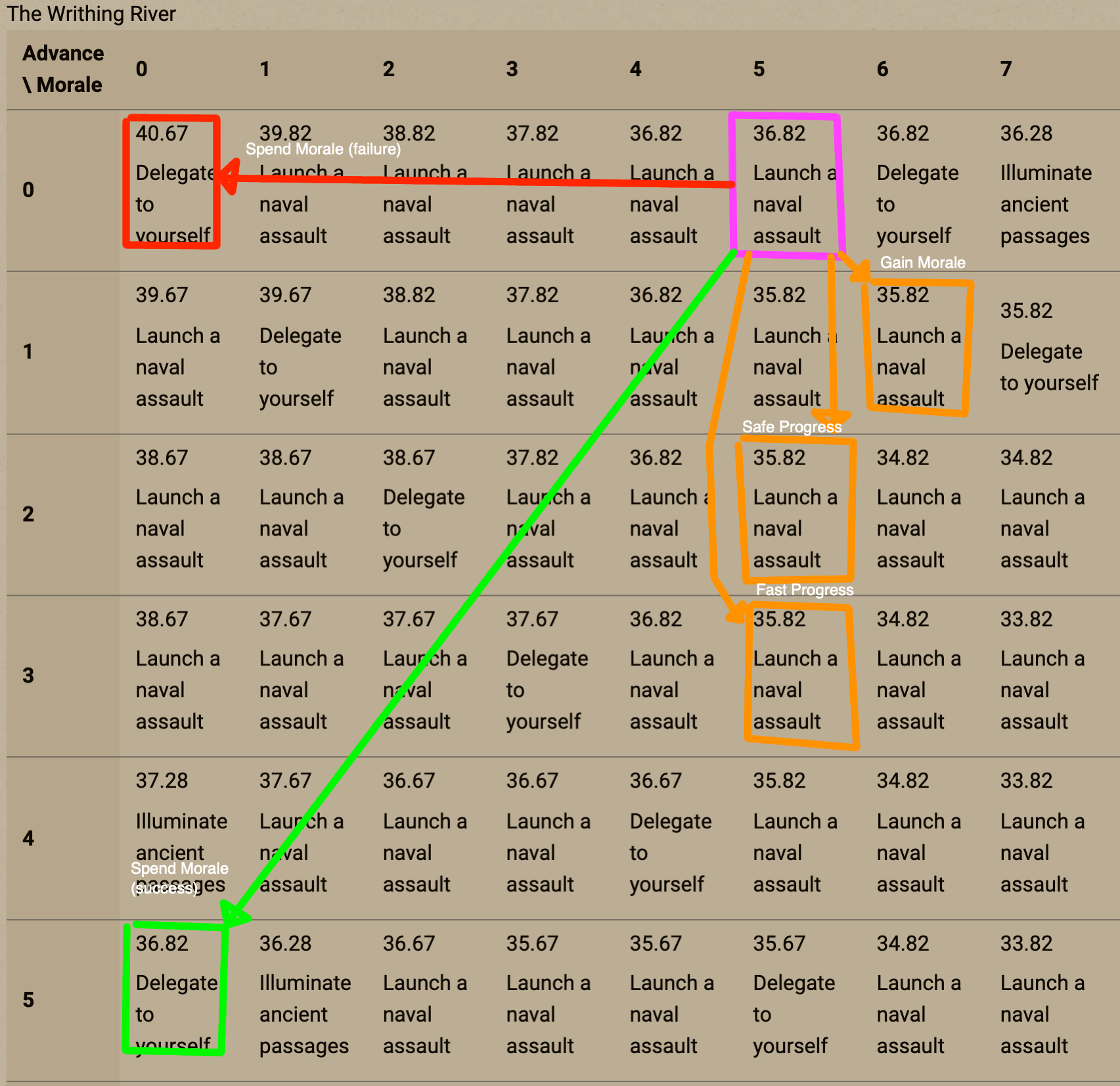
As an example, consider the table below, showing results for the Writhing River, calculated with default values. Results in the table are computed beginning from the bottom of the table going upwards, and from left to right. The cell highlighted in purple represents the campaign state of & , and the other highlighted cells indicate the outcome of all the possible actions that a player could choose from that point. The total Actions-to-Complete from each of those states in the Campaign have already been calculated. We can then compute the expected Actions-to-Complete of each of the available options by taking into account its outcomes, success probability, and resource cost. The option with the lowest expected Actions-to-Complete is recommended as the best option, and its Actions-to-Complete is stored as the value for that cell, which will be referenced by other actions that result in that game state.

From these data points, the values of each of the options available can be calculated as in the table below. Based on these, the best option available is to Gain Morale (Launch a naval assault), with an expected Actions-to-Complete of 36.82 from this point forward.

Option	Cost to Move	Result of Move	Total Actions-to-Complete
Spend Morale	1 Action	36.82 on success (100%)	37.82
		40.67 on failure (0%)
Gain Morale	1 Action	35.82	36.82
Safe Progress	1 Action Item worth 1 Action	35.82	37.82
Fast Progress	1.39 Actions Items worth 0.88 Actions Ravages worth 0.39 Actions	35.82	38.48

Calculations

Some actions (like most Safe Progress options) always produce the same amount of on success or failure, but have different resource costs. For a given Advance! a and Morale m, the Actions-to-Goal value A(a, m) can be computed as

$A(a,m)=1+A(a+1,m)+p\times c_{s}+(1-p)\times c_{f}$

where p is the probability of success, and c_s and c_f are the resource costs of success and failure. The constant 1 is the action spent on playing the option. The value A(a+1, m) is the Actions-to-Goal for one more Advance! and the same Morale; some actions may add more Advance!.

Spending Morale is a slightly different situation, where success & failure both always spend Morale but one only gives Advance!. For this situation, the formula is modified slightly. Note that no Morale options cost resources, so the c terms are ignored.

$A(a,m)=1+p\times A(a+5,m-5)+(1-p)\times A(a,m-5)$

Most other options work slightly differently, where costs are accrued on failure but neither Advance! nor Morale is modified. If such an option is the best choice, then it should be attempted repeatedly until successful. In these cases, the formula can be derived by observing that with a success probability p, one success will require 1/p attempts and incur ( 1/p - 1) failures.

$A(a,m)={\frac {1}{p}}+A(a+3,m)+c_{s}+({\frac {1}{p}}-1)\times c_{f}$

As before, the a + 3 term is an example for early-stage Fast Progress options, but other options modify Advance! and Morale in different ways.

Airs

The impact of Airs-dependent options are tricky to account for. They cannot always be attempted, which is straightforward to accommodate. The more difficult issue is that on failure, sometimes the option can be re-attempted and sometimes it cannot.

The Actions-to-complete value for an Airs option A_a(a, m) depends in part on the value for the best deterministic option available, A_d(a, m). With a success probability s, and assuming Airs options are available exactly 1/3 of the time, the value A_a(a, m) can be calculated as:

${\begin{aligned}A_{a}(a,m)={\frac {2}{3}}&\left(A_{d}(a,m)\right)\\+{\frac {1}{3}}&\left[s\times (1+A(a+4,m))+(1-s)\times \left(1+c_{f}+A_{a}(a,m)\right)\right]\end{aligned}}$

This equation defines A_a in terms of itself, which represents re-attempting on failure. The term that does not contain A_a encapsulates the fact that the option is not always available to re-attempt. Solving this recurrence relationship for a closed-form value of A_a yields the following:

$A_{a}(a,m)={\frac {2A_{d}(a,m)+s\times A(a+4,m)+c_{f}\times (1-s)+1}{2+s}}$

The Airs-dependent option should be taken if it has a better Action-to-Goal value than the determenistic options available, when $A_{a}<A_{d}$, i.e. when $A_{d}-A_{a}>0$. By substituting terms, we found Airs-dependent actions should be played when the following is true:

$A(a+4,m)<A_{d}(a,m)-{\frac {1+c_{f}\times (1-s)}{s}}$

The fraction on the right describes how much better the success result of the Airs option needs to be compared to the best deterministic option in order to be worth playing.

When there are multiple Airs-dependent options available, the same analysis will produce equations which have more terms but are not significantly more complicated. This analysis will slightly under-value Airs-dependent options when the best deterministic option can be re-attempted on failure, because it does not account for the possibility that failures of the deterministic option might allow the Airs option to become available again.